Euclid

"It is of course not surprising that, in these days of short cuts, there should have arisen a movement to get rid of Euclid and to substitute a “royal road to geometry”; the marvel is that a book which was not written for schoolboys but for grown men should have held its own as a school-book for so long…
It was with reference to such a danger that Dionysius Lardner wrote in 1846:
“Euclid once superseded, every teacher would esteem his own work the best, and every school would have its own class book. All that rigour and exactitude which have so long excited the admiration of men of science would be at an end. These very words would lose all definite meaning. Every school would have a different standard; matter of assumption in one being matter of demonstration in another; until, at length, GEOMETRY, in the ancient sense of the word, would be altogether frittered away or be only considered as a particular application of Arithmetic and Algebra.”
It is, perhaps, too early yet to prophesy what will be the ultimate outcome of the new order of things; but it would at least seem possible that history will repeat itself and that, when chaos has come again in geometrical teaching, there will be a return to Euclid more or less complete for the purpose of standardising once more...
Euclid’s work will live long after all the text-books of the present day are superseded and forgotten. It is one of the noblest monuments of antiquity…"
Sir Thomas L. Heath - 'Euclid - The Thirteen Books of the Elements' Vol I ‘preface’ November 1908

I heartily concur with Sir Thomas Heath’s prophetic observation and Dionysius Lardner's 1846 statement regarding the dangerous confusions and misunderstandings that the abandonment of Euclid will lead us toward. At the time of his writing Sir Thomas could have had no conception that the ‘chaos’ he prophesied in mathematics was likely to permeate the relatively modern science of ‘biological-chemistry’, and hence the whole of science and society in general. Sad to say, since 1953, the present understanding of DNA structure has single handedly sent education, truth and knowledge on a wrong headed trajectory. To coin a phrase, it would seem that we, the generality of the people, have been led right royally up the garden path as they say, and theretofore, humanity now finds itself in an all consuming state of ignorence - scientific, cultural, and educational.
The ancient practice of ‘geometry' that so many people find dry, dull and difficult, serves a very key purpose. It both prises open and exercises the mind in a very stringent manner - similar to the good that today we might ascribe to physical exercise on the body. Evidently our reluctance to engage with Euclid is nothing new, for even Peregrine Pickle, the eponymous and comic hero of Tobias Smollett’s 18th Century comic novel, when introduced to ‘Euclid’s tests of truth by demonstration’, found that his head drooped and his interest waned on contemplation of the ‘pons asinorum’ [BI.pr5] and ‘Pythagoras’s discovery that the square of the hypotenuse was equal to the squares of the other two sides of a right-angled triangle’[BI.pr47]. The final propositions of Euclid’s thirteenth book [XIII.pr13-18] deal with the Platonic solids which I have illustrated below. These were 3-D in form and, to some extent, were the springboard for what Plato termed our woeful lack of investigation into Solid Geometry [Republic - Education of the Philosopher 528, bcde]. Plato had a tendency to scoff at the visual arts in general, but only, I suspect, because the Ancients never fully understood Mathematical Linear Perspective, a device which came to light during the early Renaissance. Whilst the ancient’s understood perspective in the simplistic sense of recession - ie the foreground larger and the background smaller - they never corollated the two as a direct mathematical progression. Had they done so I don’t doubt there would likely have been a fourteenth book containing many 3-D geometric propositions. One of those propositions would likely have been the Pentagonal Helix that I happen to stumble over in 1995 when trying to resolve considerable topological problems with regard to Crick and Watson’s proposed and accepted model.
To the biochemist who will question the importance of geometry and who places all their emphasis on the chemistry of molecules I can but press them to contemplate the spacial illustration on the cover of one of their own Bibles (below). An atom is by its very nature a ‘monad’, and ‘compound groups of monads’ create molecules of both 2 and 3-dimensional geometric space and structure. Is it really so unreasonable to argue that the proportion, regularity and dynamic abilities exhibited by the DNA ‘super-molecule’ are in large part equally accounted for by geometric shape and structure as well as by the chemical attractions and interactions of their parts?

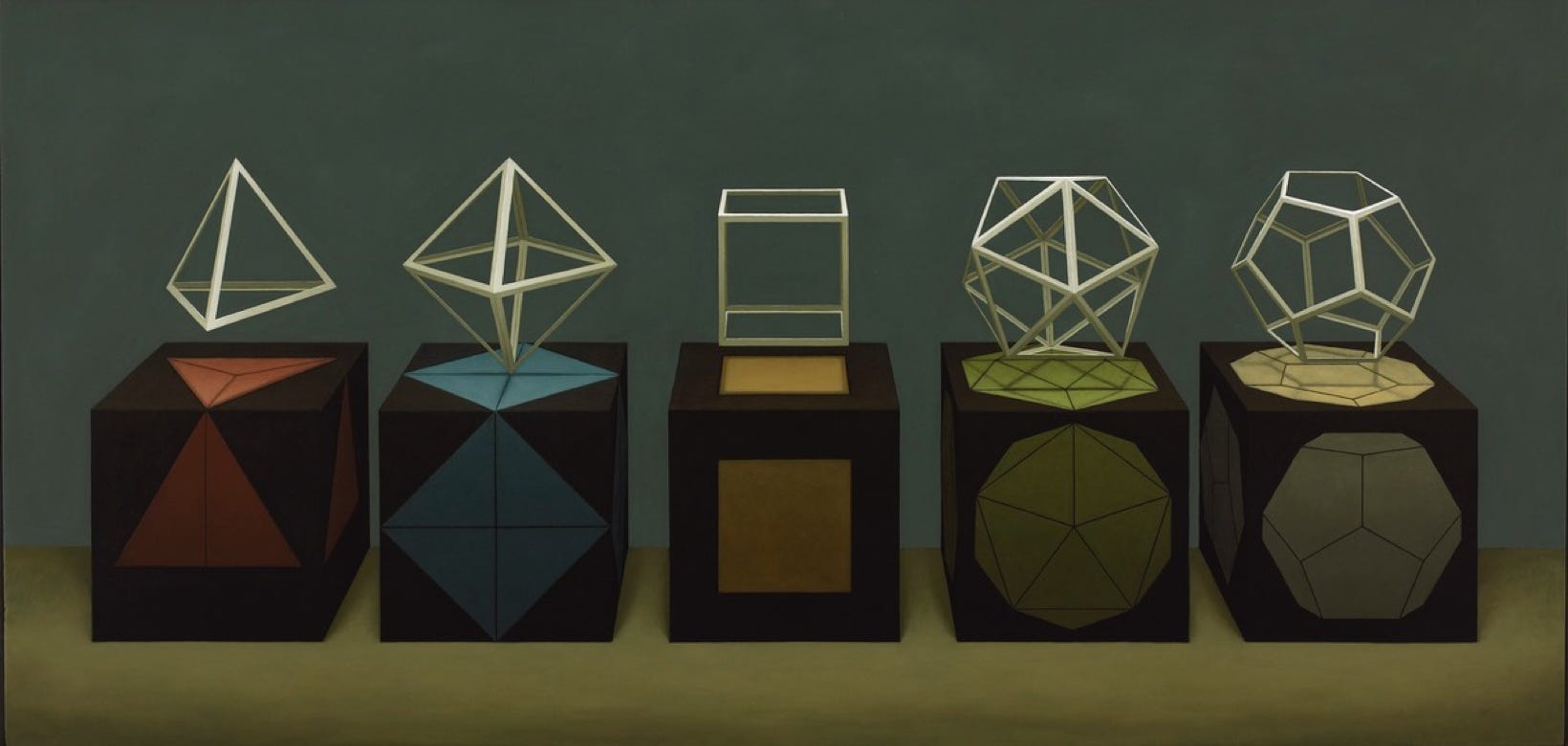
Tetrahedron - Octahedron - Cube - Icosahedron - Dodecahedron
Platonic Solids
Oil on panel
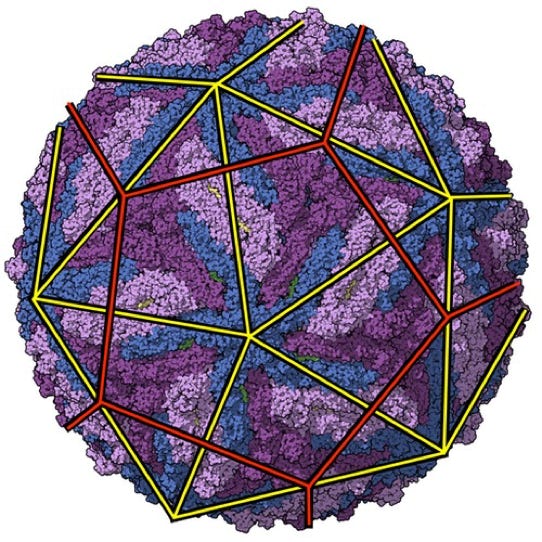
Furthermore, if geometry really doesn’t play a part in the architecture of molecules and subsequent super-molecules, I would ask how it is that so many viruses, phytoplankton and diatom’s accurately exhibit structural combinations and variations of just such pure geometric architecture.
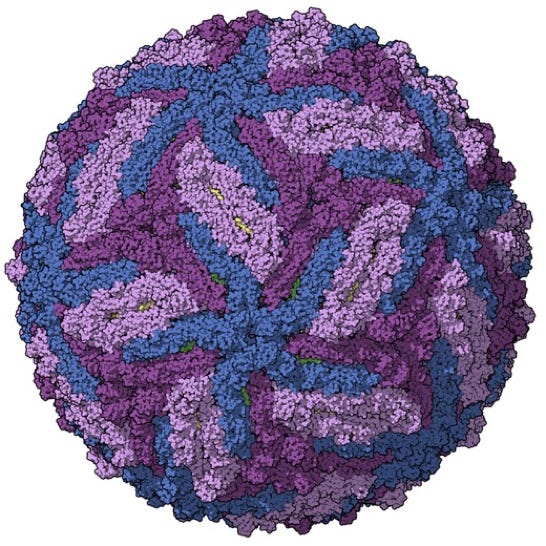
Zika Virus
Icosahedron & Dodecahedron
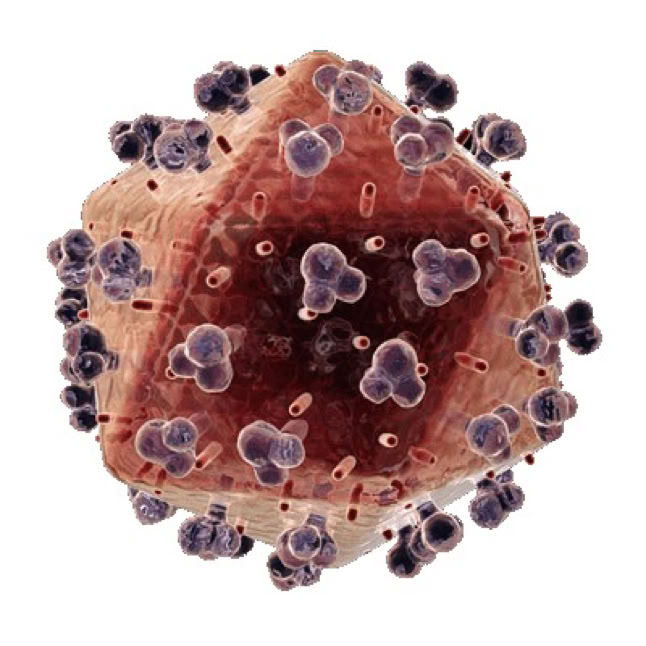
Yellow Fever Virus
Icosahedron
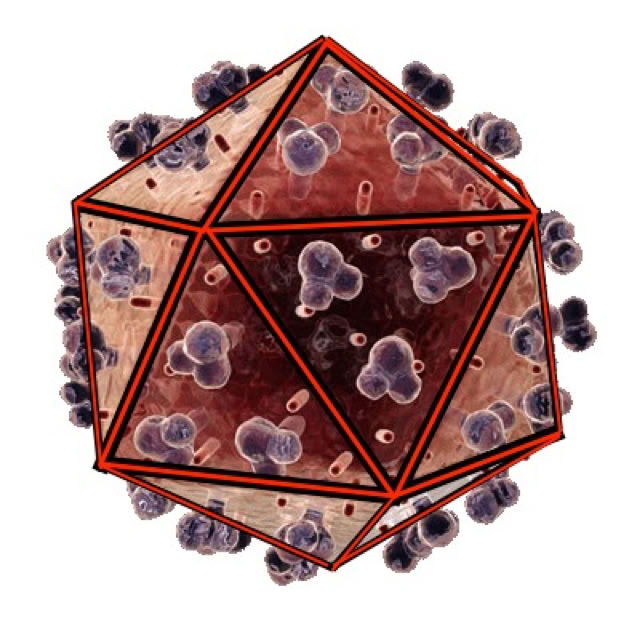
Cowpea Mosaic Virus
Icosahedron


Foot & Mouth Virus
Icosahedron & Dodecahedron
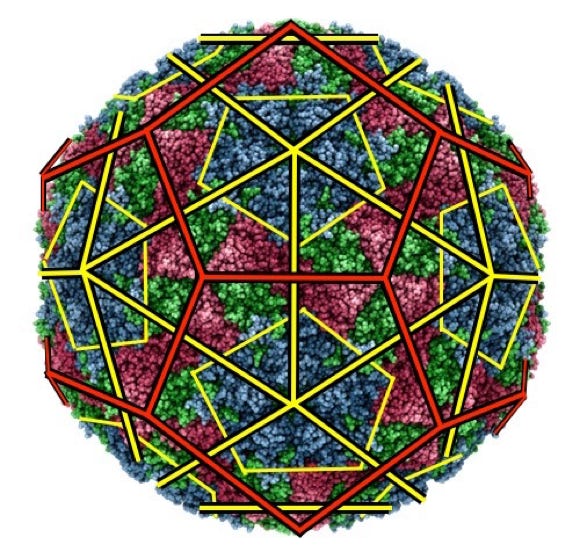
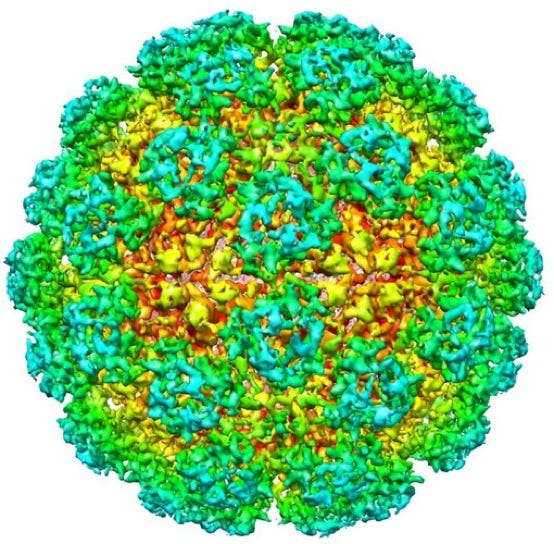
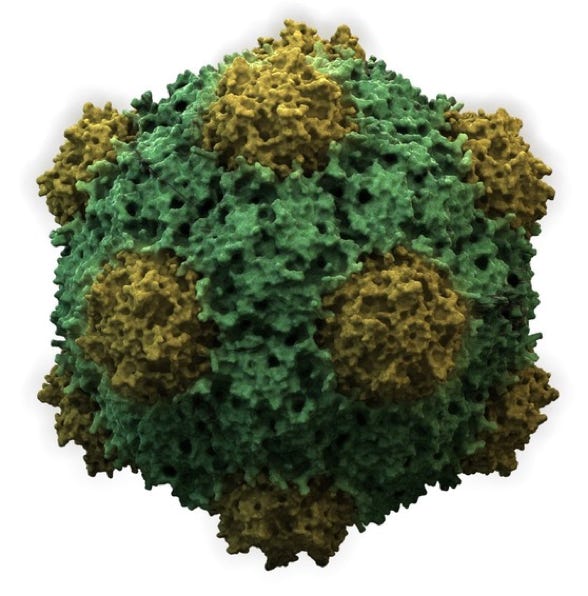
Nematode Orsay Virus
Truncated Icosahedron
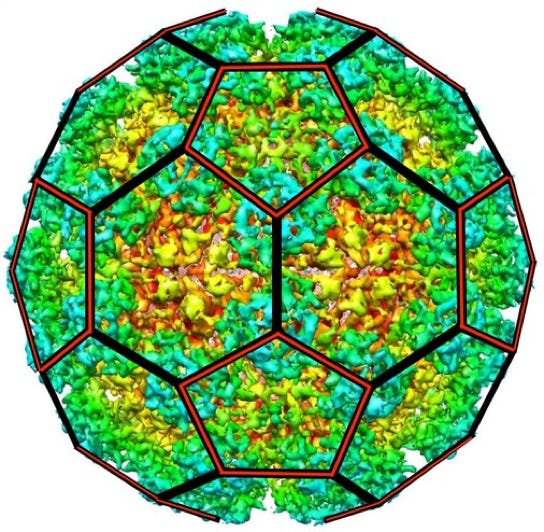
Grouper Nervous Necrosis Virus
Truncated Icosahedron
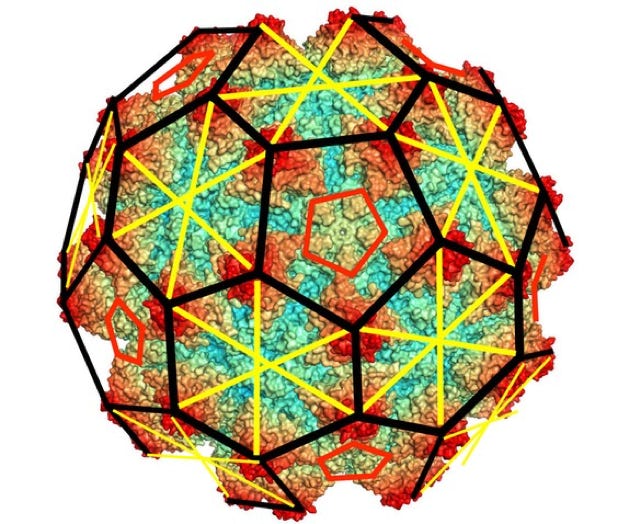
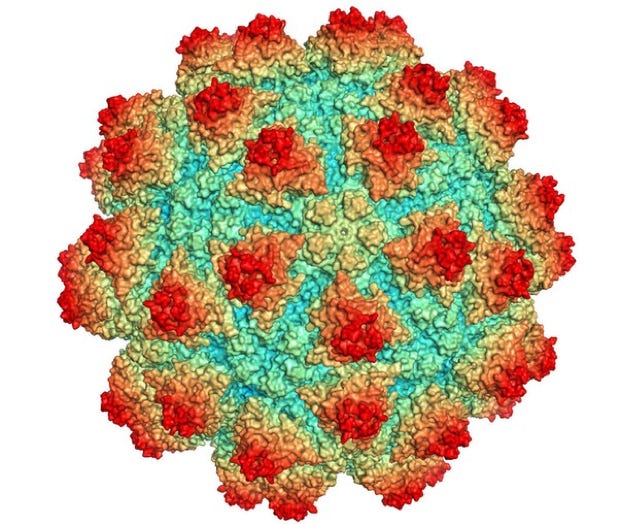
Polio Virus
Icosahedron & Dodecahedron
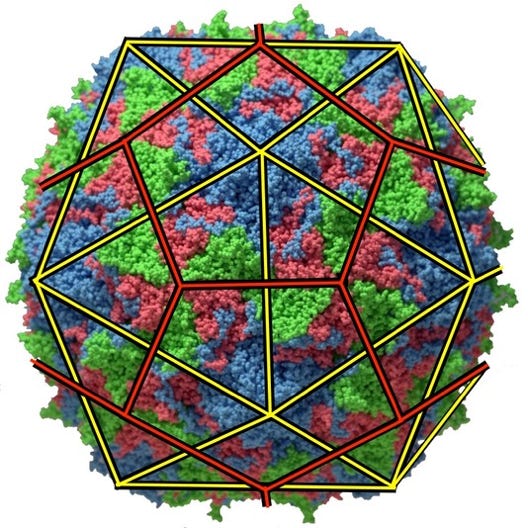
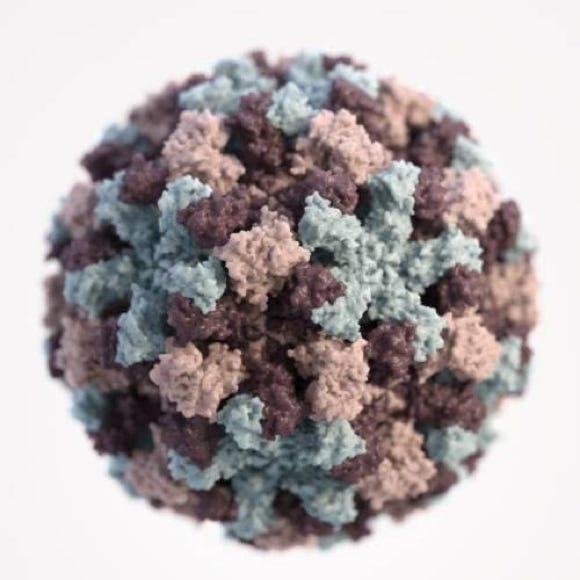
Noro Virus
Variation


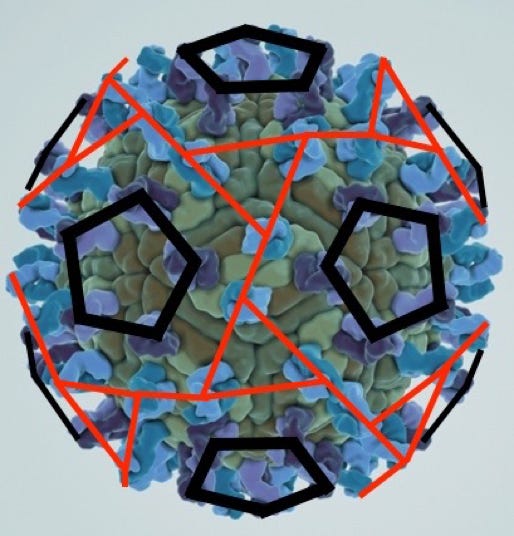
West Nile Virus
Variation
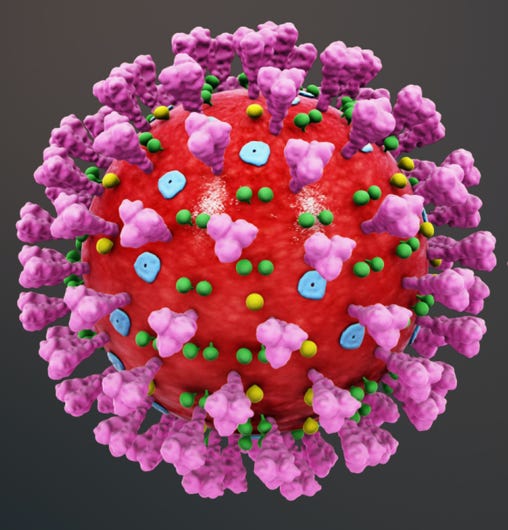

Covid 19
Truncated Icosahedron
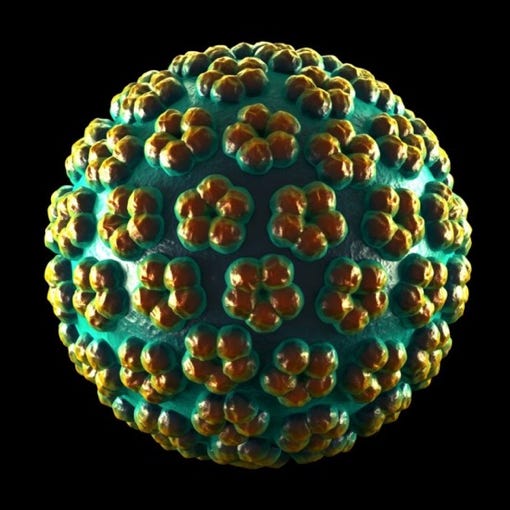
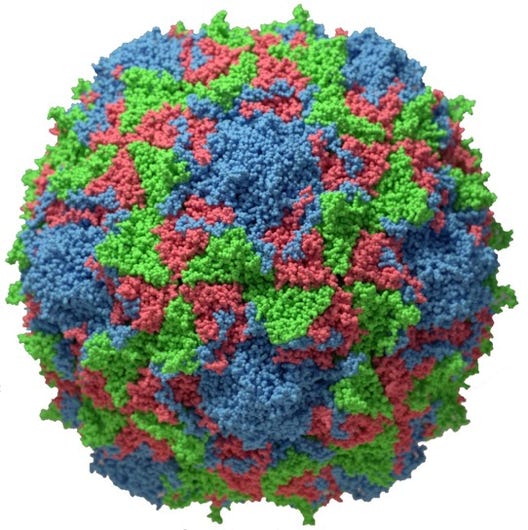
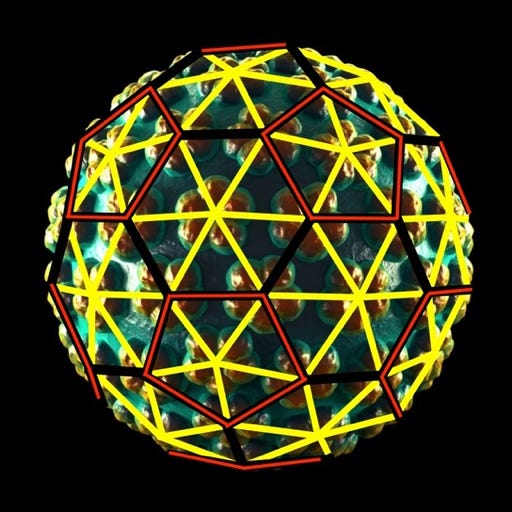
Human Papilloma Virus
Truncated Icosahedron
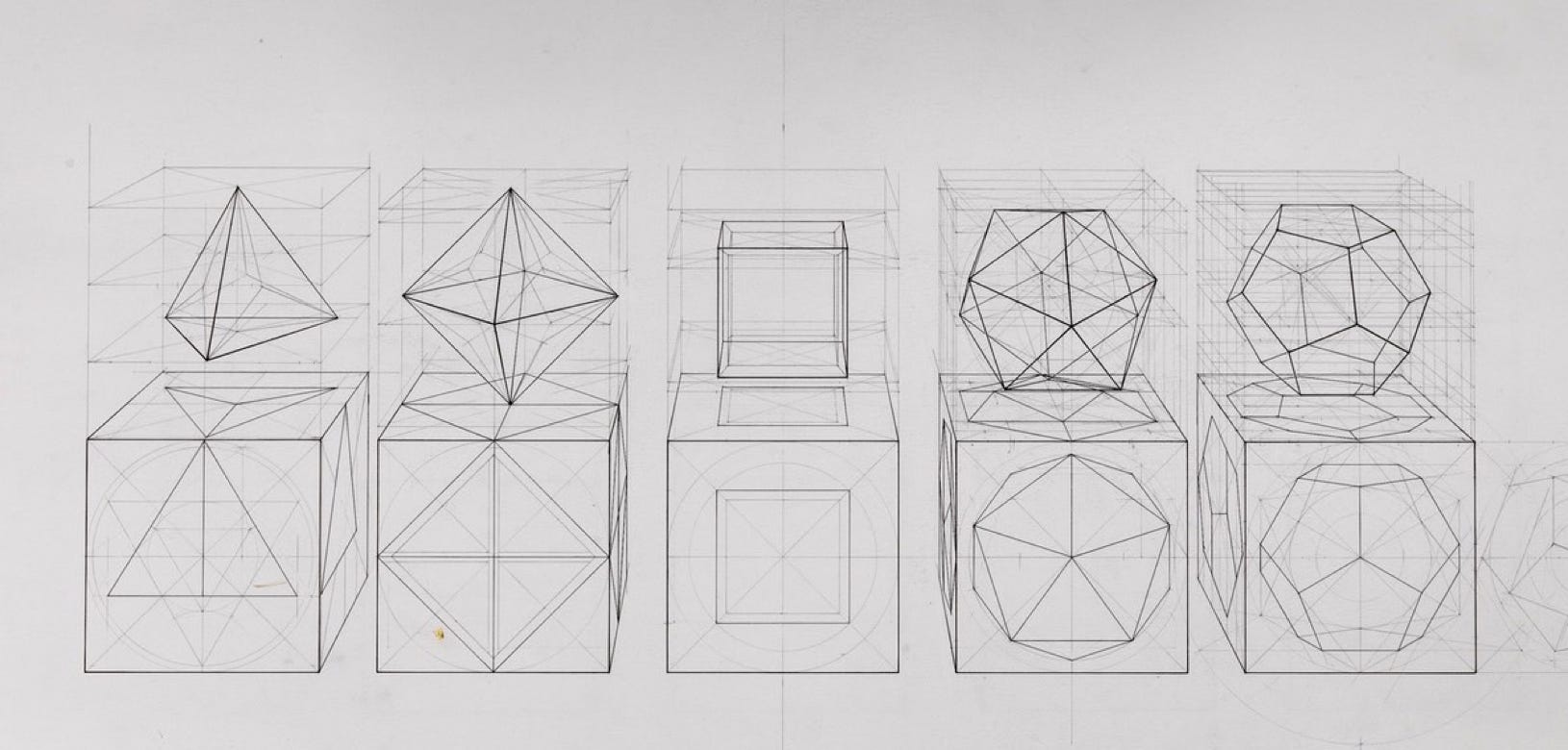
Tetrahedron - Octahedron - Cube - Icosahedron - Dodecahedron